Is my OBBLOG
Ignoring the equivalences of the Karnaugh table, OBBLOG contains all the possible logic gates with two inputs and one output.
This is the partial living OBBLOG Truth Table:
For to build a operating toy, I added forks, crossings at different levels and bit visualizers. (Similar to a light bulb)
However, the toy did not have flip-flops, so you could not make a numbers counter, although small binary calculators 1 to 16 bits.
The toy allows to build little and simple animated toys:
Or more complex constructions:
Binary Tree:
But from the initial basic logic gates, I discovered that it was possible to build a flip-flop:
(And consequently a counter of binary numbers):
(The obblog allows a closed loop that continues
to circulate indefinitely if not obstructed)
(without flip-flops)
I posted all this, because yesterday I found similar artifacts along the history of computing:
The article published in Scientific American the December of 1964:
Fluid logic devices, all based in the Coanda effect:
(Fluidic amplifier: https://en.wikipedia.org/wiki/Fluidics)
Referred by: Fluidic computing at Bowles Fluidics:
http://strangebits.blogspot.com.es/2007/05/i-had-pleasure-of-participating-in.html
Coding and computation in microfluidics.
http://cba.mit.edu/events/07.05.fluid/
And the conference from Manu Prakash,
http://cba.mit.edu/events/07.05.fluid/Prakash.pdf
The manu Prakash Thesis: (About "microfluidic bubble logic"), and inside this beautiful Truth table about logic gates and its equivalents in transistors, valves, electrical devices, and fluidics:
Some examples of projected fluidic devices:
(from Prakash thesis)
Integrated fluidic logic gates with a schematic integrated control circuit
The main patents about fluidics, come from the sixties:
https://www.google.com/patents/US4854176
(from wikipedia)
And schema about Coanda effect from Popular Science (Jun 1967 Pag 118) :
And the: Fluidics: Basic components and applications
By: James W. Joyce (1977; Unclassified: 1983):
And from the conference:
APPLIED HYDRAULICS AND PNEUMATICS U5MEA23 Prepared by Mr. Jayavelu.S & Mr. Shri Harish Assistant Professor, Mechanical. http://slideplayer.com/slide/5675986/
I would like to see these companions of my program, running.
Anyway, everybody can see them inside the Bowles products:
And inside of the Theranos patented devices: (Lab-on-a-chip)
//////////////////////////////ADDED 2019/09/30//////////////////////////////////////
An the works of William Phillips (economist)
His contribution to Economics and Mathematics: The Phillips Curve:
William Phillips and his: MONIAC (Monetary Income Analogue Computer) Also known as: Phillips Hydraulic Computer:
William Phillips and his MONIAC
"Phillips ended up at the London School of Economics (LSE) and became
very interested in Keynesian theory. It was at this time that he built
the Moniac machine. In 1958, Phillips published his seminal work on the
relationship between inflation and unemployment. He moved back to
Australia in 1967, before passing away in Auckland in March 1975."
"At LSE [1] Phillips was interested in the circular flow of money model. With
his knowledge of hydro-mechanics, Phillips realised that he could build
a machine that would take the static circular flow model out of the
textbook and into a dynamic 3 dimensional setting, by using water to
represent the flow of money. Using a diverse range of materials
including bits and pieces from obsolete Lancaster bombers, the first
Moniac was created in his landlady’s garage. It was built at a cost of
£400 – over $32,000 in today’s money."
"The machine was unveiled in a seminar at LSE in 1949, and Phillips
explained how his machine could be used to demonstrate the complex
interrelationships between macroeconomic variables such as consumption,
taxes, government spending, investment, savings, interest rates and
exchange rates. A second machine was built to represent the rest of the
world and introduce trade flows into the domestic economy."
Making Money Flow: The MONIAC YouTube:
reservebankofnz: (Reserve Bank museum in Wellington)
From: LSE’s James Meade Archives:
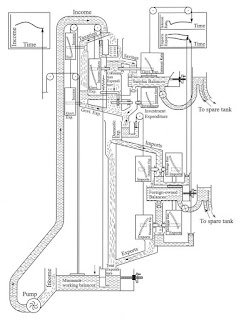
Here is a schematic drawing of MONIAC, courtesy of LSE’s James Meade Archives, with more detail explaining the machinations (From: http://nautil.us/blog/the-rube-goldberg-machine-that-mastered-keynesian-economics )
Nicholas Barr, in A.W.H. Phillips: Collected Works in Contemporary Perspective by Robert Leeson
More:
By: Andrew Adamatzky
///////////////////////////////////////////////////////////////////////////////////////////////////
More serious and basic information: Introduction to fluid Mechanics: (Dead Link)
https://vscht.cz/uchi/ped/hydroteplo/materialy/introduction.fluid.mech.pdf Y. Nakayama (1999).
(Link at Archive.org: https://web.archive.org/web/20180814192332/https://vscht.cz/uchi/ped/hydroteplo/materialy/introduction.fluid.mech.pdf )
Follow: Reflections about all this at: (Dead Link) https://plus.google.com/communities/102467630739607363236
(Link at Archive.org: https://web.archive.org/web/20190330044111/https://plus.google.com/communities/102467630739607363236 )